独極・QRコード担当の「あじな」です。
「エラー訂正編」(←またもや勝手に名付けました)に入ってから、小難しそうな匂いがプンプンしてきましたね。
でも、わかりやすい解説を続けますから、どうか、どうか、見捨てないでくださいまし。。
今回は、この「ハミング距離」と「エラー訂正能力」の関係を解説します。
エラー訂正は、与えられた符号から最も「近い」単語を選ぶことでした。
例えば、「111」と「000」の2種類しか単語として存在しない場合を想像してください。そんな中、なぜか存在しないはずの「100」という符号を受け取ったとします。
この場合、「111」と「100」の距離は「2」、「000」と「100」の距離は「1」なので、もともとの符号は「000」だとのではないかと推測(エラー訂正)することができますね。
(きっと、なにかの手違いで最初の「0」が「1」に代わってしまったのでしょう)
でも、もし受け取った符号「100」の元の符号は「111」で、二つの1が汚れで0に変わって「100」なったとしたらどうでしょうか。
先ほどのような一番近い「000」だという推測は間違ってしまうことになりますよね。
これは、「最も近い単語に修正する」という方策の弱点なのです。
正しく修復できるのは、エラーが発生した符号が元の単語の近くにある場合だけで、エラーが発生した符号が別の単語の近くまでぶっとんでしまうと元に戻せなくなります。
正確に言うと、受けとった符号が、元の符号とその近くの別の単語との距離の「半分」までの範囲ならば「エラー訂正」が可能です。
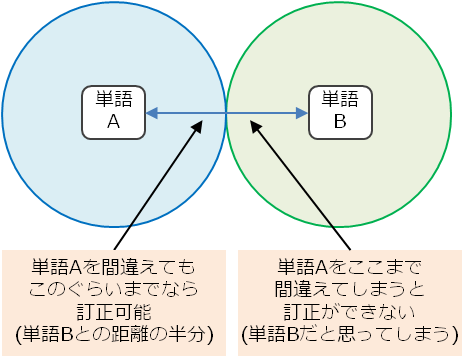
単語間の距離と訂正可能範囲
先ほどの例でいうと、「111」と「000」の距離は「3」なので、受け取った符号が、元の単語から「1.5」以上離れてしまうとエラー訂正ができなくなります。
つまり、3桁のうち1つ間違えても訂正可能なのですが、2つ間違えると訂正不可能になります。
同様に、もし単語間の距離が15だったとすると、7個まで間違えても訂正可能ですが、8個間違えると訂正不可能になります。
例えば、単語Aと単語Bの距離は10でも、単語Aと単語Cの距離は5ということもあり得ます。
その場合、単語Aと単語Bの間で訂正可能なエラーの数は4ですが、単語Aと単語Cの間だと2になります。
このようなケースの場合、単語A・B・Cの間で訂正可能なエラーの数は「2」とします。最悪のケースを考えるのですね。(超慎重派です)
つまり、単語間の中で最も距離が小さい組み合わせ(これが最小距離です!)を考え、そこで可能なエラー訂正の数がその符号の「エラー訂正可能数」なのです。
○最小距離が大きいと、表現できるパターン数は減る(使わない単語を増やす必要がある)
○最小距離が大きいと、エラー訂正能力が高い
あちらを立てればこちらが立たずの難しい関係ですね。
「エラー訂正編」(←またもや勝手に名付けました)に入ってから、小難しそうな匂いがプンプンしてきましたね。
でも、わかりやすい解説を続けますから、どうか、どうか、見捨てないでくださいまし。。
これまでの復習 [表示する]
- QRコードは株式会社デンソーが作ったもので、スマホや携帯で読み取れる
- QRコードは「小さな白と黒の四角でできている」「多少汚れても大丈夫」という特徴がある
- 白黒の四角を使うのは、コンピュータにわかりやすくさせるため
- QRコードは「機能パターン」と「符号化領域」で出来上がっている
- 「機能パターン」は、「クワイエットゾーン」「位置検出パターン」「位置検出パターンの分離パターン」「タイミングパターン」「位置合わせパターン」の5種類
- 「符号化領域」は「形式情報」「型番情報」「データ領域」の3種類
- 「形式情報」は「エラー訂正レベル」と「マスクパターン参照子」で決まり、「\(4 \times 8=32\)」種類のパターンがある
- 「型番情報」は「QRコードのバージョンによって決まり、40種類ある
- 「データ領域」は「データ」と「エラー訂正情報」で出来上がる
- QRコードはバージョンが1~40まである。一辺の大きさは、「QRコードのバージョン(1~40)\( \times \)4\( + \)17」
- 「エラー訂正レベル」は「L(7%の汚れまで)」「M(15%の汚れまで)」「Q(25%の汚れまで)」「H(30%の汚れまで)」の4種類ある。
- 「エラー訂正レベル」が「L」だと「QRコード」で表現できるデータの量は最大で、「H」のときに最小になる。
- 「1bit」とは白・黒、1・0のような2種類の情報を表すことができる能力のことで、文字を増やすと「2bit(4種類)」「3bit(8種類)」と表現できる種類が増える
- 日常の言葉を「エンコード」して「コード(符号)」に置き換え、「コード(符号)」を「デコード」して日常の言葉に戻す
- QRコードの「エンコード」方式は「数字モード」「英数字モード」「漢字モード」「8bitモード」の4種類
- どの「エンコード」方式でも、データは「モード指示子」+「文字数指示子」+「データ」+「終端パターン」+「埋め草ビット」+「埋め草ワード」となる
- QRコードには「白」と「黒」を読み間違えても、元の情報を復元する「エラー訂正」能力が備わっている
- 「エラー訂正」は読み取れた(聞き取れた)言葉から最も近い「ありえそうな単語」を推測すること
- 「エラー訂正力が強い」ということは、「あえて使っていない単語が多い」ということと同じで、効率性は悪い
- 1,0でできている符号では「ハミング距離(2つの符号間で1と0が異なる箇所の個数)」があり、符号間で最も「ハミング距離」が小さいものを「最小距離」と呼ぶ
- 使える「単語」を制限すると「最小距離」は大きくなる
見分ける能力
前回の解説で単語の間の「ハミング距離」と、単語間の中でも最も小さい距離の「最小距離」のお話しをしました。今回は、この「ハミング距離」と「エラー訂正能力」の関係を解説します。
エラー訂正は、与えられた符号から最も「近い」単語を選ぶことでした。
例えば、「111」と「000」の2種類しか単語として存在しない場合を想像してください。そんな中、なぜか存在しないはずの「100」という符号を受け取ったとします。
この場合、「111」と「100」の距離は「2」、「000」と「100」の距離は「1」なので、もともとの符号は「000」だとのではないかと推測(エラー訂正)することができますね。
(きっと、なにかの手違いで最初の「0」が「1」に代わってしまったのでしょう)
でも、もし受け取った符号「100」の元の符号は「111」で、二つの1が汚れで0に変わって「100」なったとしたらどうでしょうか。
先ほどのような一番近い「000」だという推測は間違ってしまうことになりますよね。
これは、「最も近い単語に修正する」という方策の弱点なのです。
正しく修復できるのは、エラーが発生した符号が元の単語の近くにある場合だけで、エラーが発生した符号が別の単語の近くまでぶっとんでしまうと元に戻せなくなります。
正確に言うと、受けとった符号が、元の符号とその近くの別の単語との距離の「半分」までの範囲ならば「エラー訂正」が可能です。

先ほどの例でいうと、「111」と「000」の距離は「3」なので、受け取った符号が、元の単語から「1.5」以上離れてしまうとエラー訂正ができなくなります。
つまり、3桁のうち1つ間違えても訂正可能なのですが、2つ間違えると訂正不可能になります。
同様に、もし単語間の距離が15だったとすると、7個まで間違えても訂正可能ですが、8個間違えると訂正不可能になります。
最小距離の出番
先ほどの例で「訂正可能な範囲」のイメージがついたでしょうか?ちなみに、「単語間の距離」は測定する2つの単語の選び方で変わります。例えば、単語Aと単語Bの距離は10でも、単語Aと単語Cの距離は5ということもあり得ます。
その場合、単語Aと単語Bの間で訂正可能なエラーの数は4ですが、単語Aと単語Cの間だと2になります。
このようなケースの場合、単語A・B・Cの間で訂正可能なエラーの数は「2」とします。最悪のケースを考えるのですね。(超慎重派です)
つまり、単語間の中で最も距離が小さい組み合わせ(これが最小距離です!)を考え、そこで可能なエラー訂正の数がその符号の「エラー訂正可能数」なのです。
最小距離・エラー訂正能力・パターン数
これまで、解説してきたことをまとめるとこうなります。○最小距離が大きいと、表現できるパターン数は減る(使わない単語を増やす必要がある)
○最小距離が大きいと、エラー訂正能力が高い
あちらを立てればこちらが立たずの難しい関係ですね。
