どもども。独極・QRコード担当の「あじな」です。
さぁ、今回からいよいよ「行列」を見ていきましょう。
「QRコード」を解説するつもりが、「行列」の解説の記事が一番多くなるかもしれません・・・・
行列とは「数字をならべたもの」。ただそれだけです。本当にそれだけです・・・。例えば次のようなものです。
\( \left( \begin{array}{cc}1 & 2 \end{array} \right)\\ \)・・・・01
\( \left( \begin{array}{cc}1 & 3 \\ 2 & 2 \end{array} \right)\\ \)・・・・02
\( \left( \begin{array}{c}1 \\ 2 \\ 3 \end{array} \right)\\ \)・・・・03
以上です。。。本当、以上なんです。。。
でも、意外にこれだけの行列がとっても役に立つんです。これからちょっとずつ解説しますね。
数字の横の並びのことを「行」と言います。そして、数字の縦の並びのことを「列」と言います。
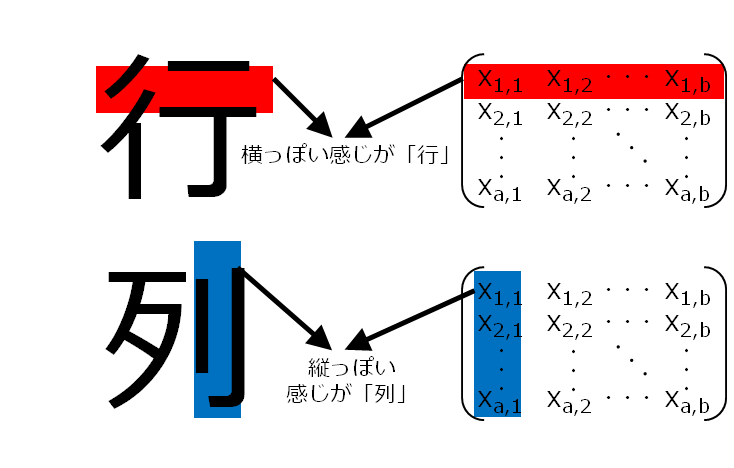
「行」「列」の覚え方
行列の大きさを表すときには「2行3列」とか言います。先ほどの例では、01の行列は「1行2列」、02の行列は「2行2列」、03の行列は「3行1列」ですね。
\begin{eqnarray} \left\{ \begin{array}{l} 3x+2y+3z \\ 5x-10y+2z \\ 2x-3y-4z \end{array} \right. \end{eqnarray} この連立方程式の\(x,y,z\)の係数を取り出したものを並べて書くと、「行列」になっちゃったんです。
$$\left( \begin{array}{ccc} 3 & 2 & 3\\ 5 & -10 & 2 \\ 2 & -3 & -4 \end{array} \right)\\ $$ こうやって書くほうが、いちいち数式を書くよりも簡単ですよね?このように、連立方程式の書き方を楽にするために、「行列」は生まれたんです。
(やり方は後でじっくり解説しますので、今はふーーんと思っておいてください)
そのほかにも、「正方行列」「転置行列」「単位行列」「余因子行列」「行列式」「逆行列」というような行列にまつわる考え方があります。
それぞれゆっくり、解説していくので、飽きずに読んでくださいね。
さぁ、今回からいよいよ「行列」を見ていきましょう。
「QRコード」を解説するつもりが、「行列」の解説の記事が一番多くなるかもしれません・・・・
これまでの復習 [表示する]
- QRコードは株式会社デンソーが作ったもので、スマホや携帯で読み取れる
- QRコードは「小さな白と黒の四角でできている」「多少汚れても大丈夫」という特徴がある
- 白黒の四角を使うのは、コンピュータにわかりやすくさせるため
- QRコードは「機能パターン」と「符号化領域」で出来上がっている
- 「機能パターン」は、「クワイエットゾーン」「位置検出パターン」「位置検出パターンの分離パターン」「タイミングパターン」「位置合わせパターン」の5種類
- 「符号化領域」は「形式情報」「型番情報」「データ領域」の3種類
- 「形式情報」は「エラー訂正レベル」と「マスクパターン参照子」で決まり、「\(4 \times 8=32\)」種類のパターンがある
- 「型番情報」は「QRコードのバージョンによって決まり、40種類ある
- 「データ領域」は「データ」と「エラー訂正情報」で出来上がる
- QRコードはバージョンが1~40まである。一辺の大きさは、「QRコードのバージョン(1~40)\( \times \)4\( + \)17」
- 「エラー訂正レベル」は「L(7%の汚れまで)」「M(15%の汚れまで)」「Q(25%の汚れまで)」「H(30%の汚れまで)」の4種類ある。
- 「エラー訂正レベル」が「L」だと「QRコード」で表現できるデータの量は最大で、「H」のときに最小になる。
- 「1bit」とは白・黒、1・0のような2種類の情報を表すことができる能力のことで、文字を増やすと「2bit(4種類)」「3bit(8種類)」と表現できる種類が増える
- 日常の言葉を「エンコード」して「コード(符号)」に置き換え、「コード(符号)」を「デコード」して日常の言葉に戻す
- QRコードの「エンコード」方式は「数字モード」「英数字モード」「漢字モード」「8bitモード」の4種類
- どの「エンコード」方式でも、データは「モード指示子」+「文字数指示子」+「データ」+「終端パターン」+「埋め草ビット」+「埋め草ワード」となる
- QRコードには「白」と「黒」を読み間違えても、元の情報を復元する「エラー訂正」能力が備わっている
- 「エラー訂正」は読み取れた(聞き取れた)言葉から最も近い「ありえそうな単語」を推測すること
- 「エラー訂正力が強い」ということは、「あえて使っていない単語が多い」ということと同じで、効率性は悪い
- 1,0でできている符号では「ハミング距離(2つの符号間で1と0が異なる箇所の個数)」があり、符号間で最も「ハミング距離」が小さいものを「最小距離」と呼ぶ
- 使える「単語」を制限すると「最小距離」は大きくなる
- 「最小距離」の半分までのエラーであれば訂正することができる
- 「単語」を「符号化」したものに、適当な「1」や「0」を後ろにつけると「最小距離」が大きい「エラー訂正機能付符号」になる
- 「エラー訂正機能付符号」を作る際は「符号」に「行列(生成行列)」を掛け算する。
- 「QRコード」は「リード・ソロモン符号」と呼ばれる方法で「エラー訂正機能付符号」を作る
数字を並べる。それが行列
まずは、行列とはなんぞやというふかーーい真理について解説しようと思ったのですが、意外に行列は単純です。行列とは「数字をならべたもの」。ただそれだけです。本当にそれだけです・・・。例えば次のようなものです。
\( \left( \begin{array}{cc}1 & 2 \end{array} \right)\\ \)・・・・01
\( \left( \begin{array}{cc}1 & 3 \\ 2 & 2 \end{array} \right)\\ \)・・・・02
\( \left( \begin{array}{c}1 \\ 2 \\ 3 \end{array} \right)\\ \)・・・・03
以上です。。。本当、以上なんです。。。
でも、意外にこれだけの行列がとっても役に立つんです。これからちょっとずつ解説しますね。
行列の用語
行列の紹介だけでは、単純すぎるので、行列で使われる「言葉」も解説しておきます。数字の横の並びのことを「行」と言います。そして、数字の縦の並びのことを「列」と言います。

行列の大きさを表すときには「2行3列」とか言います。先ほどの例では、01の行列は「1行2列」、02の行列は「2行2列」、03の行列は「3行1列」ですね。
「行列」の誕生理由?
「行列」は、その昔し、次のような連立方程式を簡単に記述する方法として考えられました。\begin{eqnarray} \left\{ \begin{array}{l} 3x+2y+3z \\ 5x-10y+2z \\ 2x-3y-4z \end{array} \right. \end{eqnarray} この連立方程式の\(x,y,z\)の係数を取り出したものを並べて書くと、「行列」になっちゃったんです。
$$\left( \begin{array}{ccc} 3 & 2 & 3\\ 5 & -10 & 2 \\ 2 & -3 & -4 \end{array} \right)\\ $$ こうやって書くほうが、いちいち数式を書くよりも簡単ですよね?このように、連立方程式の書き方を楽にするために、「行列」は生まれたんです。
「行列」の「足し算」・「引き算」・「掛け算」・「割り算」を学ぼう
行列は、行列同士の「足し算」、「引き算」、「掛け算」、「割り算」(この四つを合わせて「四則演算」と呼びます)ができるようになっています。(やり方は後でじっくり解説しますので、今はふーーんと思っておいてください)
そのほかにも、「正方行列」「転置行列」「単位行列」「余因子行列」「行列式」「逆行列」というような行列にまつわる考え方があります。
それぞれゆっくり、解説していくので、飽きずに読んでくださいね。
