独極・QRコード担当の「あじな」です。
どんどんすすめていきましょう。今回は「行列の掛け算」です。
行列の掛け算は、エラー訂正機能付符号の計算に必須のアイテムです。
例えば、エラー訂正機能付符号(これも、1行n列の行列とみなせます)に「検査行列」というものを「掛け算」すると、その結果がゼロ行列(要素の全てが0の行列)になるといった関係性がでてきます。
そのため、是非、行列の掛け算のやり方を覚えてくださいね。
百聞は一見に如かず。といいますし、まずは例を見てみましょう。(どうして、私のパソコンは「例」と書こうとすると「霊」と変換されるのでしょうか・・・。ちょっと怖い。)
$$ \begin{pmatrix} 5 & 3 \\ 1 & 2 \end{pmatrix} \times \begin{pmatrix} 9 \\ 4 \end{pmatrix}=\begin{pmatrix} 5 \times 9+3 \times 4 \\ 1 \times 9+2 \times 4 \end{pmatrix}=\begin{pmatrix} 57 \\ 17 \end{pmatrix} $$ どうです。不思議でしょ?この式を見て、「行列」の「掛け算」の規則わかりますか?
行列の掛け算は「STEP1 掛け算した結果の行列の大きさを決める」「STEP2 掛け算した結果の行列の各要素の値を求める」という2つのステップで計算していきます。
まず、STEP1として掛け算した結果の行列の大きさ(サイズ)を決めます。
掛け算した結果の行列のサイズは、掛け算の「左側の行列」の「行数(上の場合は、2行)」と、「右側の行列」の「列数(上の場合は、1列)」になると決められております。(上の例だと、2行1列の行列)
まず、このサイズの求め方をしっかりと覚えましょう。
次に、STEP2として求めたサイズの大きさの行列の各要素を1つ1つ求めていきます。
まず、答えの「行列」の「1行1列目」の要素を計算します。
1行1列目の要素を求めるには「掛け算」に出てくる「左側の行列」の「1行目」(上の例だと、\(\begin{pmatrix} 5 & 3 \end{pmatrix}\))と「右側の行列」の「1列目」に着目します。(上の例だと、\(\begin{pmatrix} 9 \\ 4 \end{pmatrix}\))に注目します。
この二つの「要素同士」を「掛け算」したものを「足し合わせ」ます。(上の例だと、\( 5 \times 9+3 \times 4\)です)
この結果が、答えの行列の1行1列目になります。
次に、答えの「行列」の「2行1列目」の要素を計算します。
「左側の行列」の「2行目」(上の例だと、\(\begin{pmatrix} 1 & 2 \end{pmatrix}\))と「右側の行列」の「1列目」に着目します。(上の例だと、\(\begin{pmatrix} 9 \\ 4 \end{pmatrix}\)で)
この二つの「要素同士」を「掛け算」したものを「足し合わせ」ます。(上の例だと、\( 1 \times 9+2 \times 4\)になります )
この結果が、答えの行列の2行1列目になります。
このように、左の「行列」から「行」をとってきて、右の「行列」から「列」をとってきて、それぞれの要素をかけ合わせ合計する方法で、答えの「行列」の各要素を計算していくと、「掛け算」の完成です。
ここで注意してほしいことは、左の「行列」の1行に含まれる要素の数と、右の「行列」の1列に含まれる要素の数が同じである必要があるということです。(違うと、それぞれの要素を掛け合わせるときに、相手がいない要素がでてしまいます)
このことはつまり、行列の掛け算を考えるときには左の「行列」の「列数(列数は1行に含まれる要素の数と同じ)」と右の「行列」の「行数(行数は1列に含まれる要素の数と同じ)」が同じである必要があるということです。
そうすると、左の「行列」の大きさが「a行b列」で、右の「行列」の大きさが「b行c列」だった時、「掛け算」結果の行列は「a行c列」になります。(bは左と右の「行列」で同じ必要がありましたね)。
図示するとちょっとわかりやすいでしょうか。
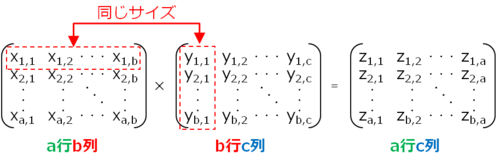
行列の掛け算イメージ
$$ \begin{pmatrix} 5 & 3 \\ 1 & 2 \end{pmatrix} \times \begin{pmatrix} 9 & 2 & 3 \\ 4 & 1 & 2 \end{pmatrix}=\begin{pmatrix} 5 \times 9+3 \times 4 & 5 \times 2+3 \times 1 & 5 \times 3+3 \times 2 \\ 1 \times 9+2 \times 4 & 1 \times 2+2 \times 1 & 1 \times 3+2 \times 2 \end{pmatrix}=\begin{pmatrix} 57 & 13 & 21 \\ 17 & 4 & 7 \end{pmatrix} $$ $$ \begin{pmatrix} 1 & 2 & 2 \\ 3 & 2 & 5 \end{pmatrix} \times \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix}=\begin{pmatrix} 1 \times 2+2 \times 3+2 \times 1 \\3 \times 2+2 \times 3+5 \times 1 \end{pmatrix}=\begin{pmatrix} 10 \\ 17 \end{pmatrix} $$ 計算のイメージを掴んでいただけましたでしょうか?
次回は、この不思議な「行列」の「掛け算」の規則について簡単に解説します。
どんどんすすめていきましょう。今回は「行列の掛け算」です。
行列の掛け算は、エラー訂正機能付符号の計算に必須のアイテムです。
例えば、エラー訂正機能付符号(これも、1行n列の行列とみなせます)に「検査行列」というものを「掛け算」すると、その結果がゼロ行列(要素の全てが0の行列)になるといった関係性がでてきます。
そのため、是非、行列の掛け算のやり方を覚えてくださいね。
これまでの復習 [表示する]
- QRコードは株式会社デンソーが作ったもので、スマホや携帯で読み取れる
- QRコードは「小さな白と黒の四角でできている」「多少汚れても大丈夫」という特徴がある
- 白黒の四角を使うのは、コンピュータにわかりやすくさせるため
- QRコードは「機能パターン」と「符号化領域」で出来上がっている
- 「機能パターン」は、「クワイエットゾーン」「位置検出パターン」「位置検出パターンの分離パターン」「タイミングパターン」「位置合わせパターン」の5種類
- 「符号化領域」は「形式情報」「型番情報」「データ領域」の3種類
- 「形式情報」は「エラー訂正レベル」と「マスクパターン参照子」で決まり、「\(4 \times 8=32\)」種類のパターンがある
- 「型番情報」は「QRコードのバージョンによって決まり、40種類ある
- 「データ領域」は「データ」と「エラー訂正情報」で出来上がる
- QRコードはバージョンが1~40まである。一辺の大きさは、「QRコードのバージョン(1~40)\( \times \)4\( + \)17」
- 「エラー訂正レベル」は「L(7%の汚れまで)」「M(15%の汚れまで)」「Q(25%の汚れまで)」「H(30%の汚れまで)」の4種類ある。
- 「エラー訂正レベル」が「L」だと「QRコード」で表現できるデータの量は最大で、「H」のときに最小になる。
- 「1bit」とは白・黒、1・0のような2種類の情報を表すことができる能力のことで、文字を増やすと「2bit(4種類)」「3bit(8種類)」と表現できる種類が増える
- 日常の言葉を「エンコード」して「コード(符号)」に置き換え、「コード(符号)」を「デコード」して日常の言葉に戻す
- QRコードの「エンコード」方式は「数字モード」「英数字モード」「漢字モード」「8bitモード」の4種類
- どの「エンコード」方式でも、データは「モード指示子」+「文字数指示子」+「データ」+「終端パターン」+「埋め草ビット」+「埋め草ワード」となる
- QRコードには「白」と「黒」を読み間違えても、元の情報を復元する「エラー訂正」能力が備わっている
- 「エラー訂正」は読み取れた(聞き取れた)言葉から最も近い「ありえそうな単語」を推測すること
- 「エラー訂正力が強い」ということは、「あえて使っていない単語が多い」ということと同じで、効率性は悪い
- 1,0でできている符号では「ハミング距離(2つの符号間で1と0が異なる箇所の個数)」があり、符号間で最も「ハミング距離」が小さいものを「最小距離」と呼ぶ
- 使える「単語」を制限すると「最小距離」は大きくなる
- 「最小距離」の半分までのエラーであれば訂正することができる
- 「単語」を「符号化」したものに、適当な「1」や「0」を後ろにつけると「最小距離」が大きい「エラー訂正機能付符号」になる
- 「エラー訂正機能付符号」を作る際は「符号」に「行列(生成行列)」を掛け算する。
- 「QRコード」は「リード・ソロモン符号」と呼ばれる方法で「エラー訂正機能付符号」を作る
- 行列は数字を並べただけのもので、もともとは「連立方程式」の係数だけ抜き取ってならべたもの
- 行列の「足し算」「引き算」は各「行列」の要素同士を「足し算」「引き算」したもの
行列の掛け算はそのまんま「じゃない!」
「行列」の「足し算」・「引き算」と異なって、「掛け算」は風変りなことをするんです。百聞は一見に如かず。といいますし、まずは例を見てみましょう。(どうして、私のパソコンは「例」と書こうとすると「霊」と変換されるのでしょうか・・・。ちょっと怖い。)
$$ \begin{pmatrix} 5 & 3 \\ 1 & 2 \end{pmatrix} \times \begin{pmatrix} 9 \\ 4 \end{pmatrix}=\begin{pmatrix} 5 \times 9+3 \times 4 \\ 1 \times 9+2 \times 4 \end{pmatrix}=\begin{pmatrix} 57 \\ 17 \end{pmatrix} $$ どうです。不思議でしょ?この式を見て、「行列」の「掛け算」の規則わかりますか?
行列の掛け算は「STEP1 掛け算した結果の行列の大きさを決める」「STEP2 掛け算した結果の行列の各要素の値を求める」という2つのステップで計算していきます。
まず、STEP1として掛け算した結果の行列の大きさ(サイズ)を決めます。
掛け算した結果の行列のサイズは、掛け算の「左側の行列」の「行数(上の場合は、2行)」と、「右側の行列」の「列数(上の場合は、1列)」になると決められております。(上の例だと、2行1列の行列)
まず、このサイズの求め方をしっかりと覚えましょう。
次に、STEP2として求めたサイズの大きさの行列の各要素を1つ1つ求めていきます。
まず、答えの「行列」の「1行1列目」の要素を計算します。
1行1列目の要素を求めるには「掛け算」に出てくる「左側の行列」の「1行目」(上の例だと、\(\begin{pmatrix} 5 & 3 \end{pmatrix}\))と「右側の行列」の「1列目」に着目します。(上の例だと、\(\begin{pmatrix} 9 \\ 4 \end{pmatrix}\))に注目します。
この二つの「要素同士」を「掛け算」したものを「足し合わせ」ます。(上の例だと、\( 5 \times 9+3 \times 4\)です)
この結果が、答えの行列の1行1列目になります。
次に、答えの「行列」の「2行1列目」の要素を計算します。
「左側の行列」の「2行目」(上の例だと、\(\begin{pmatrix} 1 & 2 \end{pmatrix}\))と「右側の行列」の「1列目」に着目します。(上の例だと、\(\begin{pmatrix} 9 \\ 4 \end{pmatrix}\)で)
この二つの「要素同士」を「掛け算」したものを「足し合わせ」ます。(上の例だと、\( 1 \times 9+2 \times 4\)になります )
この結果が、答えの行列の2行1列目になります。
このように、左の「行列」から「行」をとってきて、右の「行列」から「列」をとってきて、それぞれの要素をかけ合わせ合計する方法で、答えの「行列」の各要素を計算していくと、「掛け算」の完成です。
ここで注意してほしいことは、左の「行列」の1行に含まれる要素の数と、右の「行列」の1列に含まれる要素の数が同じである必要があるということです。(違うと、それぞれの要素を掛け合わせるときに、相手がいない要素がでてしまいます)
このことはつまり、行列の掛け算を考えるときには左の「行列」の「列数(列数は1行に含まれる要素の数と同じ)」と右の「行列」の「行数(行数は1列に含まれる要素の数と同じ)」が同じである必要があるということです。
そうすると、左の「行列」の大きさが「a行b列」で、右の「行列」の大きさが「b行c列」だった時、「掛け算」結果の行列は「a行c列」になります。(bは左と右の「行列」で同じ必要がありましたね)。
図示するとちょっとわかりやすいでしょうか。

ちょこっと掛け算の練習
「行列」の「掛け算」の例をいくつか書きますので、計算のイメージをつかんでくださいね。$$ \begin{pmatrix} 5 & 3 \\ 1 & 2 \end{pmatrix} \times \begin{pmatrix} 9 & 2 & 3 \\ 4 & 1 & 2 \end{pmatrix}=\begin{pmatrix} 5 \times 9+3 \times 4 & 5 \times 2+3 \times 1 & 5 \times 3+3 \times 2 \\ 1 \times 9+2 \times 4 & 1 \times 2+2 \times 1 & 1 \times 3+2 \times 2 \end{pmatrix}=\begin{pmatrix} 57 & 13 & 21 \\ 17 & 4 & 7 \end{pmatrix} $$ $$ \begin{pmatrix} 1 & 2 & 2 \\ 3 & 2 & 5 \end{pmatrix} \times \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix}=\begin{pmatrix} 1 \times 2+2 \times 3+2 \times 1 \\3 \times 2+2 \times 3+5 \times 1 \end{pmatrix}=\begin{pmatrix} 10 \\ 17 \end{pmatrix} $$ 計算のイメージを掴んでいただけましたでしょうか?
次回は、この不思議な「行列」の「掛け算」の規則について簡単に解説します。
